Пересечение высот в треугольнике, Точка пересечения высот треугольника

Это довольно простое следствие теоремы Пифагора. Например, доказать, что они являются биссектрисами какого-то треугольника, или серединными перпендикулярами, или медианами главное при этом не попасть в порочный круг. Дело в том, что высоты являются биссектрисами ортотреугольника. А вот как.
Nathan Altshiller-Court. Параграф: G. The Orthopole. Одесса, Высоты треугольника. Теорема Архимеда. Carroll, Elyn Rykken.

Geometry: The Line and the Circle неопр. Дата обращения: 10 апреля Second Edition. Прямоугольный Равнобедренный Равносторонний Равнобедренный прямоугольный.
Неравенство треугольника Признаки подобия треугольников Решение треугольников Теорема о внешнем угле треугольника Теорема о сумме углов треугольника Теорема Пифагора Теорема косинусов Теорема синусов Теорема о проекциях Формула Герона. Сферический треугольник Гиперболический треугольник Симплекс. Категории : История математики Замечательные точки треугольника Точки в Энциклопедии центров треугольника. Пространства имён Статья Обсуждение.
Скачать как PDF Версия для печати.
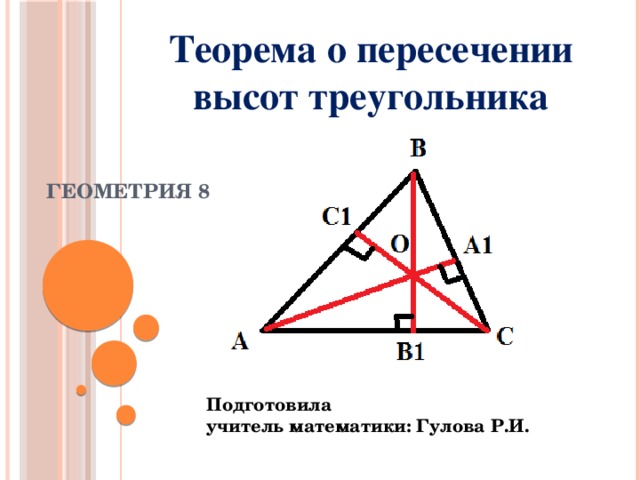
Точка пересечения прямых, содержащих высоты треугольника, называется его ортоцентром. Это одна из так называемых замечательных точек треугольника наравне с точкой пересечения медиан, биссектрис и серединных перпендикуляров треугольника.
Задачи от мистера Фокса.

По теореме о сумме углов треугольника,. Меню Подобрать занятия. Учебник Избранные статьи. Скачайте мобильное приложение и читайте Фоксфорд Учебник на телефоне и планшете. Точка пересечения высот. Сложность статьи Подготовиться к ЕГЭ. Заметим, что: - треугольник является тупоугольным тогда и только тогда, когда его ортоцентр лежит вне треугольника; - треугольник является остроугольным тогда и только тогда, когда его ортоцентр лежит внутри треугольника; - треугольник является прямоугольным тогда и только тогда, когда его ортоцентр совпадает с вершиной прямого угла треугольника.
Дано и решение.
Понятно 29 Непонятно 4. Войдите или зарегистрируйтесь , чтобы голосовать. А еще вы сможете сохранять статьи в «избранное» и смотреть видеоуроки.

Следующая статья. Выбирайте, что поможет вам достичь целей. Я — Мистер Фокс, ваш онлайн-помощник. Ответьте на несколько вопросов, а я помогу за 5 минут подобрать подходящие варианты обучения.